MATEMÁTICAS Y DIDÁCTICA DE LAS MATEMÁTICAS II: PUNTO DE INTERSECCIÓN

DETERMINA EL PUNTO DE INTERSECCIÓN DE LOS SIGUIENTES PROBLEMAS

EJERCICIO NÚMERO 1:

* LA RECTA QUE PASA POR (-1,5), m= -2/3, Y LA RECTA 4x+y-11= 0.

Y2 - Y1

m= ---------------

X2 - X1

y - 5

- 2/3 = ---------------

x - ( -1 )

y - 5

- 2/3 = ---------------

x + 1

- 2/3 ( x + 1) = y - 5

- 2/3x - 2/3 = y - 5

- 2/3x - 2/3 - y + 5 = 0

- 2/3x + 4 1/3- y = 0 ( -1 )

2/3x + y - 13/3 = 0

4 x + y - 11 = 0

                y = - 4 x + 11

                2/3 x + y - 13/3 = 0

2/3 x + (- 4 x + 11) - 13/3 = 0

      2/3 x - 4 x + 11 - 13/3 = 0

               - 3 1/3 x + 6 2/3 = 0

                           - 3 1/3 x = - 6 2/3

                                               - 6 2/3
                                       x = --------------
                                                 - 3 1/3

                                       x = 2

    4 x + y - 11 = 0

4 ( 2 ) + y - 11 = 0

       8 + y - 11 = 0

             - 3 + y = 0

                      y = 3

( 2, 3 )

COMPROBACIÓN

2/3 x + y - 13/3 = 0 4 x + y - 11 = 0

2/3 ( 2) + 3 - 13/3 = 0 4 ( 2 ) + 3 - 11 = 0

4/3 + 3 - 13/ 3 = 0 8 + 3 - 11 = 0

13/3 - 13/ 3 = 0 11 - 11 = 0

0 = 0 0 = 0

* OTRA MANERA DE SOLUCIONAR ESTA ECUACIÓN ES:

Y2 - Y1

m= ---------------

X2 - X1

y - 5

- 2/3 = ---------------

x - (-1)

y - 5

- 2/3 = ---------------

x + 1

- 2/3 ( x + 1) = y - 5

     -    2x - 2
        -----------   = y - 5
              3

- 2x - 2 = y - 5 ( 3 )

- 2x - 2 = 3y - 15

- 2x - 3y - 2 + 15 = 0

- 2x - 3y + 13 = 0       ( -1 )

2x + 3y - 13 = 0

        2x + 3y - 13 = 0
     ( 4x + y - 11 = 0 )     ( - 3 )
--------------------------------------
        2x ~~+ 3 y~~ - 13 = 0
    - 12x ~~- 3 y~~ + 33 = 0
--------------------------------------
    - 10 x        + 20 = 0

                    - 10x = - 20

                                   - 20
                          x = --------
                                   - 10

                          x = 2

    2x + 3y - 13 = 0

2 ( 2 ) + 3y - 13 = 0

      4 + 3y - 13 = 0

              3 y - 9 = 0

                    3 y = 9

                               9
                      y = ------
                               3

                      y = 3

( 2 , 3 )

COMPROBACIÓN

      4x + y - 11 = 0

4 ( 2 ) + 3 - 11 = 0

       8 + 3 - 11 = 0

           11 - 11 = 0

                    0 = 0

VIDEO: PUNTO DE INTERSECCIÓN DE DOS RECTAS

EJERCICIO NÚMERO 2:

* DETERMINA LOS PUNTOS DE INTERSECCIÓN DE LAS SIGUIENTES ECUACIONES:

11 x + y -17 = 0 Y 5 x + 3y - 23 = 0

11x + y - 17 = 0
y = - 11x + 17

                  5x + 3y - 23 = 0

5x + 3 ( - 11x + 17) -23 = 0

        5x - 33x + 51 - 23 = 0

                     - 28x + 28 = 0

                             - 28x = - 28

                                          - 28
                                   x = -------
                                          - 28

                                   x = 1

    11x + y - 17 = 0

11 ( 1 ) + y - 17 = 0

        11 + y - 17 = 0

                  y - 6 = 0

                       y = 6

( 1, 6 )

COMPROBACIÓN

11x + y - 17 = 0 5x + 3y - 23 = 0

11 ( 1 ) + 6 - 17 = 0 5 ( 1 ) + 3 ( 6 ) - 23 = 0

11 + 6 - 17 = 0 5 + 18 - 23 = 0

17 - 17 = 0 23 - 23 = 0
0 = 0 0 = 0

RECTAS QUE PASAN POR UN PUNTO (PUNTO DE INTERSECCIÓN)

Determinar las rectas del plano que pasan por el punto $(x_0, y_0) \,$ .
La ecuación de la recta ha de ser, como ya se sabe:

$y = m x + b \,$

Y ha de pasar por el punto $(x_0, y_0) \,$ , luego tendrá que cumplirse:

$y_0 = m x_0 + b \,$

Despejando b, tenemos esta ecuación:

$b= y_0 - m x_0 \,$

Sustituyendo b en la ecuación general de la recta:

$y = m x + (y_0 - m x_0) \,$

Ordenando términos:

$y = m (x- x_0) + y_0 \,$

Esta ecuación define un haz de rectas en el plano que pasa por el punto

(x 0, y 0)

, el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.

Recta que pasa por dos puntos

Si ha de pasar por dos puntos

(x 1, y 1)

(x 2, y 2)

luego tendrá que cumplirse

$y_{1} = m x_{1} + b \,$

$y_{2} = m x_{2} + b \,$

que forman un sistema de dos ecuaciones con dos incógnitas, las incógnitas son m y b, para resolver este sistema, cambiamos de signo a la segunda ecuación y sumando las dos ecuaciones:

$y_1 - y_2 = m x_1 - m x_2 \,$

agrupando términos:

$y_1 - y_2 = m (x_1 - x_2) \,$

despejando m:

$m= \cfrac{y_1 - y_2}{x_1 - x_2} \,$

este valor, m, es el de la pendiente de la recta que pasa por los dos puntos:

(x 1, y 1)

(x 2, y 2)

Despejando ahora el valor de b de una de las ecuaciones del sistema, por ejemplo de la primera, tenemos:

$b = y_1 - m x_1 \,$

y sustituyendo m, por su valor ya calculado;

$b = y_1 - \cfrac{y_1 - y_2}{x_1 - x_2} \; x_1 \,$

Tenemos las dos incógnitas m y b despejadas, en función de las coordenadas de los dos puntos por los que tienen que pasar, la ecuación general de la recta, con los parámetros ya calculados es:

$y = \cfrac{y_1 - y_2}{x_1 - x_2} \; x + y_1 - \cfrac{y_1 - y_2}{x_1 - x_2} \; x_1 \,$

DETERMINA EL PUNTO DE INTERSECCIÓN DE LAS SIGUIENTES ECUACIONES.

x + y - 3 = 0 Y 2x + y - 6 = 0

( x + y - 3 = 0 ) ( -1)

2x + y - 6 = 0

-----------------------------------------

- x ~~- y~~ + 3 = 0

2x ~~+ y~~ - 6 = 0

-----------------------------------------

x - 3 = 0

x = 3

x + y - 3 = 0

3 + y - 3 = 0

y = 0

( 3 , 0 )

COMPROBACIÓN

2x + y - 6 = 0

2 ( 3 ) + 0 - 6 = 0

6 - 6 = 0y

0 = 0

DETERMINA EL PUNTO DE INTERSECCIÓN DE LAS SIGUIENTES ECUACIONES.

2x + y - 5 = 0 Y 5 x + y - 2 = 0

2x + y - 5 = 0 5x + y - 2 = 0

y = - 2x + 5 y = - 5x + 2

- 2x + 5 = - 5x + 2

- 2x + 5 + 5x - 2 = 0

- 2x + 5x + 5 - 2 = 0

3x + 3 = 0

3x = - 3

- 3

x = ----------

x = - 1

5x + y - 2 = 0

5 ( -1 ) + y - 2 = 0

- 5 + y - 2 = 0

y - 7 = 0

y = 7

( - 1 , 7 )

COMPROBACIÓN

        2x + y - 5 = 0

2 ( - 1 ) + 7 - 5 = 0
        - 2 + 7 - 5 = 0

                7 - 7 = 0

                     0 = 0

MATEMÁTICAS Y DIDÁCTICA DE LAS MATEMÁTICAS II

PUNTO DE INTERSECCIÓN

Recta que pasa por dos puntos

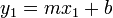
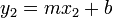
No hay comentarios:

Publicar un comentario

Datos personales